Gambling is a risky hobby to have, but haven’t we all pictured ourselves at the Bellagio or Caesar’s Palace counting cards like Mike Ross and totally killing it at Blackjack? But as the notorious saying goes, Casino Rule 1: The house always wins.
With millions of dollars on the line daily, how do casinos still remain profitable? The answer lies in simple probability and statistics!
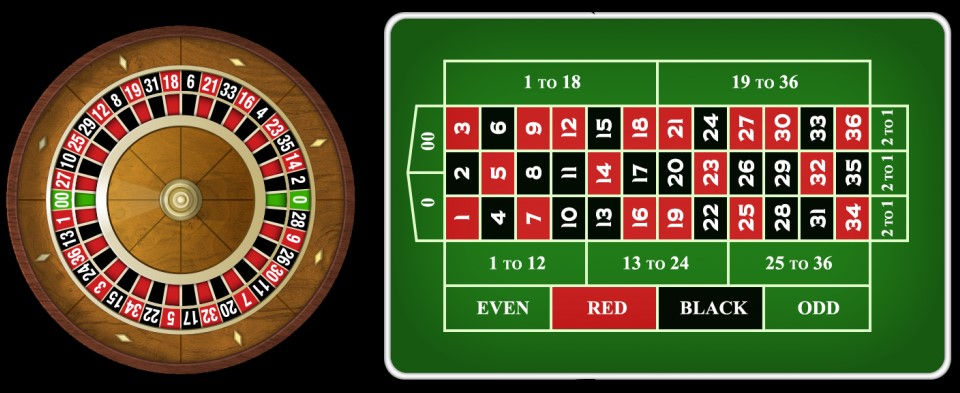
Let’s consider the example of American Roulette.
There are 38 numbers in all: 18 black, 18 red and 2 green (0 and 00) and every player at the table plays against the house. Simply put, whenever you lose, the house will win. Players may put their chips either on a single bet or on a combination of bets. Next, the dealer will spin the roulette wheel. Once the ball drops into one of the numbered pockets on the wheel, the dealer identifies and announces the winning number. The dealer marks the number on the roulette table using a dolly (a marker). All players with winning bets are subsequently paid while losing bets are swept off the table.
Let's say you want to bet on a black number. Using simple probability, the odds of you winning would be 18/38=0.474. But the house wins if the ball lands on red (18) or green (2). Hence probability that the house wins is 20/38=0.526. This extra 0.052 chance is called the "casino-edge" which is always positive for all combinations shown on the roulette table.
Now for every 1$ bet made, the house will gain roughly 5.2% i.e. 5.2 cents. Here's where the Law of Large Numbers comes into play. For every 1000 bets made, let's stick to our calculations and assume that the house loses 474 bets and wins 526 bets. Net revenue in that case would be $526-$474=$52. The University of Las Vegas has found that over 10,000 bets are made daily at roulette tables in casinos, this implies a revenue of over $520,000 from American Roulette alone.
The Law of Large Numbers theorizes that the average of a large number of results closely mirrors the expected value, and that difference narrows as more results are introduced. The Monte Carlo simulation used in data science works on a similar principle, that's why it is observed that larger the amount of input data in the algorithm, more accurate is the result.
This concept also finds use in actuarial science, i.e. insurance policies. With a large number of policyholders, the actual loss per event will break even over time.
Now you know, it never really was 50-50, you've been playing a rigged game!
Comentarios